KPK Smart Syllabus PDF

Solution of a Quadratic Equation in One Variable by Factorisation

Solution of a Quadratic Equation in One Variable by Completing Square

Solution of a Quadratic Equation by Using Quadratic Formula

Solution of the Equations of the Type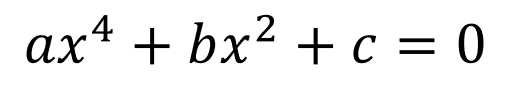

Solution of the Equations of the Type a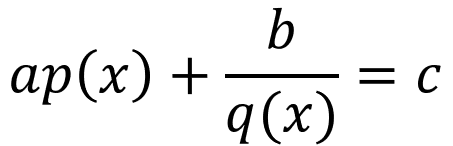

Solution of the Reciprocal Equations of the Type a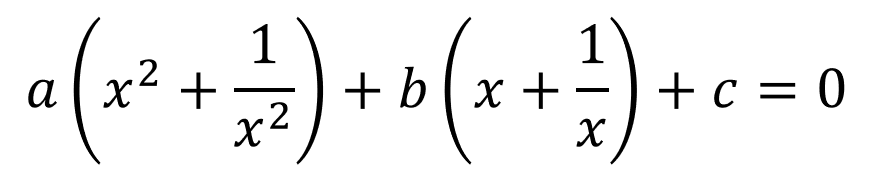

Solution of Exponential Equations Involving Variables in Exponents

Solution of the Equations of the Type 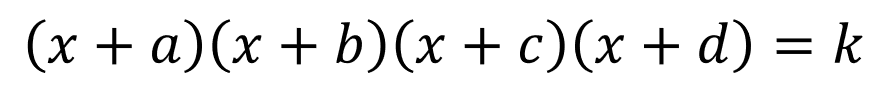, where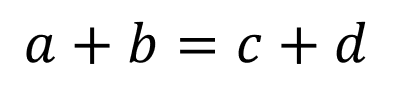

Solution of the Radical Equations of the Type: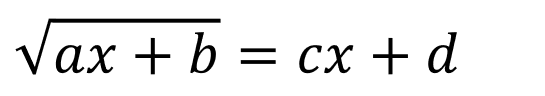

Solution of the Radical Equation of the Type: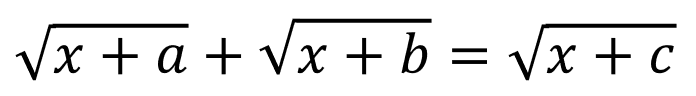

Solution of the Radical Equation of the Type: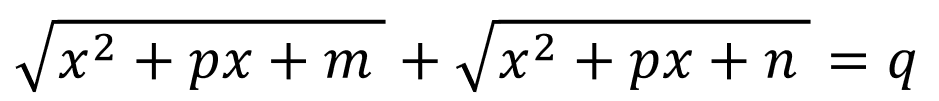

Discriminant of Quadratic Equations

Determine the Nature of Roots of a Given Quadratic Equation

Value of an Unknown Involved in a Given Quadratic Equation When the Nature of Its Roots Is Given

Use Properties of Cube Roots of Unity to Solve Appropriate Problems

Relation Between the Roots and the Coefficients of a Quadratic Equation

Values of Unknowns Involved in a Given Quadratic Equation When Sum of Roots Is Equal to a Multiple of the Products of Roots

Values of Unknowns Involved in a Given Quadratic Equation When the Sum of the Squares of Roots Is Equal to a Given Number

Values of Unknowns Involved in a Given Quadratic Equation When Roots Differ by a Given Number

Values of Unknowns Involved in a Given Quadratic Equation When Roots Satisfy a Given Relation

Values of Unknowns Involved in a Given Quadratic Equation When Both Sum and Products of Roots Are Equal to a Given Number

Formula to Find a Quadratic Equation From the Given Roots

Formation of a Quadratic Equation Whose Roots Are of the Type: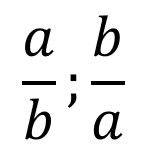

Formation of a Quadratic Equation Whose Roots Are of the Type: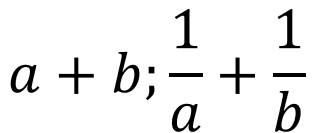

Introduction to Synthetic Division

Using Synthetic Division when Zeros of a Polynomial are Given

Using Synthetic Division when Factors of a Polynomial are Given

Using Synthetic Division to Solve a Biquadratic Equation

Solution of Simultaneous Equations with One Linear and One Quadratic Equation

Solution of Quadratic Simultaneous Equations

Solution of Real Life Problems Leading to Quadratic Equations

Ratio, Proportions, and Variations

3rd, 4th, and Mean Proportional

Theorems on Proportions

Joint Variations

K-Method

Real Life Problems Based on Variations

Resolution of Algebraic Fractions into Partial Fractions - I

Resolution of Algebraic Fractions into Partial Fractions - II

Resolution of Algebraic Fractions into Partial Fractions - III

Resolution of Algebraic Fractions into Partial Fractions - IV

Operation on Sets

Commutative and Associative Laws of Union

Commutative and Associative Laws of Intersection

Distributive Law of Union Over Intersection

Distributive Law of Intersection Over Union

De Morgan's Laws

Use Venn Diagram to Verify Commutative and Associative Laws of Union

Use Venn Diagram to Verify Commutative and Associative Laws of Intersection

Use Venn Diagram to Verify Distributive Laws

Use Venn Diagram to Verify De Morgan's Laws

Binary Relation

Function and Its Domain, Co-domain, and Range

Into Function

Injective Function

Surjective Function

Bijective Function

Examine Whether a Given Relation is a Function or Not

Grouped Frequency Table

Histograms

Frequency Polygon

Cumulative Frequency Table

Cumulative Frequency Polygon

Arithmetic Mean

Median, Mode, Geometric Mean, and Harmonic Mean

Estimate Median, Quartiles and Mode Graphically

Range, Variance, and Standard Deviation

Conversion of Angles

Relationship Between Radians and Degrees

Formula for the Length of a Circular Arc

Formula for the Area of a Circular Sector

Coterminal Angles

Quadrants and Quadrantal Angles

Values of Trigonometric Ratios for 45°, 30° and 60°

Signs of Trigonometric Ratios in Different Quadrants

Values of Remaining Trigonometric Ratios if One Trigonometric Ratio Is Given

Values of Trigonometric Ratios for 0°, 90°, 180°, 270° and 360°

Trigonometric Identities

Angles of Elevation and Depression

Triangle Theorem:

One and Only One Circle Can Pass Through Three Non-Collinear Points

A Straight Line, Drawn From the Centre of a Circle to Bisect a Chord Is Perpendicular to the Chord (and Vice Versa)

If Two Chords of a Circle Are Congruent, Then They Will Be Equidistant From the Centre (and Vice Versa)

If a Line Is Drawn Perpendicular to a Radial Segment of a Circle at Its Outer End Point, It Is Tangent to the Circle at That Point (and Vice Versa)

The Two Tangents Drawn to a Circle From a Point Outside It, Are Equal in Length

If Two Arcs of a Circle Are Congruent, Then the Corresponding Chords Are Equal (and Vice Versa)

Equal Chords of a Circle Subtend Equal Angles at the Corresponding Centres (and Vice Versa)

The Angle in a Semicircle Is a Right Angle

The Angle in a Segment Greater Than a Semi Circle Is Less Than a Right Angle (and Vice Versa)

Circumscribe a Circle About a Given Triangle

Inscribe a Circle in a Given Triangle

Escribe a Circle in a Given Triangle

Inscribe an Equilateral Triangle in a Given Circle

Circumscribe a Square About a Given Circle

Inscribe a Square in a Given Circle

Circumscribe a Regular Hexagon About a Given Circle

Inscribe a Regular Hexagon in a Given Circle

Draw a Tangent to an Arc Through a Given Point Without Using the Centre

Draw a Tangent to a Circle From a Point on or Outside the Circle

Draw Transverse Common Tangents to Two Equal Circles

Draw Direct Common Tangents to Two Unequal Circles

Draw a Circle Touching Both the Arms of a Given Angle